Mission
Madeleine est séquestrée dans un bâtiment tenu secret dans la ville de Nancy. Ses ravisseurs veulent qu’elle dévoile le secret des macarons
de Nancy. Madeleine réussit à communiquer avec toi grâce à son smartphone, qui est malheureusement non localisable.
Trouve la position exacte de Madeleine afin de venir la délivrer !

Complément : DOCUMENT 1 - Chronomètres déclenchés par Madeleine

Méthode : Mesurer une distance de manière indirecte
Mesurer une distance de propagation d’un son de manière indirecte, c’est déterminer cette distance à partir de la mesure de la durée de propagation du son et de la connaissance de sa vitesse de propagation :
\(\text{Distance de propagation} = \text{Vitesse de propagation} \times \text{Durée de propagation}\)
Trouver la position de Madeleine
Le son se propage dans toutes les directions depuis sa source et forme des cercles centrés sur la source sonore. Pour visualiser ce phénomène, regarder l’animation Son et appuyer sur le bouton vert.
Savoir utiliser une échelle graphique sur un plan
Une échelle graphique permet de passer d’une distance sur un plan à la distance réelle ou l’inverse.
Exemple :![]()
Ce segment de longueur 2 cm indique que 2 cm sur le plan correspond à une distance réelle de 50 m.
Connaître la vitesse de propagation du son
Milieu | Vide | Air | Eau | Verre |
|---|---|---|---|---|
Vitesse de propagation du son (en m/s) | 0 | 340 | 1 500 | 5 300 |
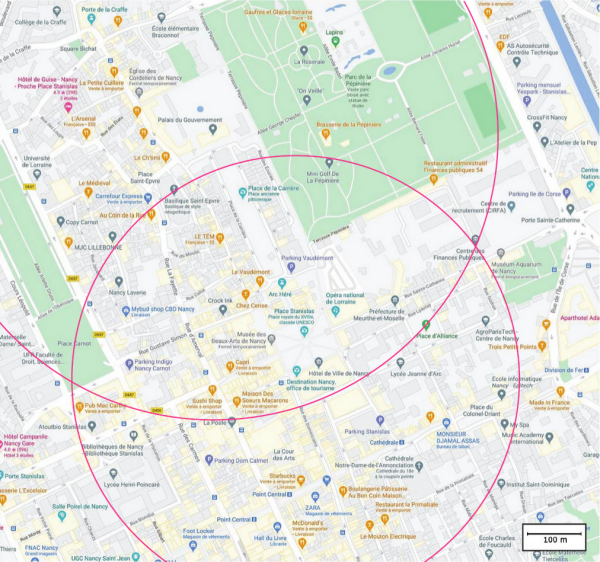
Plan d’une partie de la ville de Nancy
Question⚓
Rédige un compte rendu en expliquant la démarche suivie :
Solution⚓
La distance parcourue par le signal sonore déclenché à 13h00 est :\(d_1 = v \times t = 340 \times 1{,}57 = 534 \mathrm{m}\).
Or 2,8 cm sur le plan correspond à 100 m en réel. Ainsi les 534 m réel correspondent à une distance \(d^{'}_1 = 534 \times \frac{2,8}{100} = 14,9 \mathrm{cm}\).
Comme les ondes sonores se propagent dans toutes les directions à partir de la source sonore, il faut tracer sur la carte un cercle de rayon 14,9 cm à partir du Palais du gouvernement.
On procède de la même manière pour le signal sonore déclenché à 14h00 : \(d_2 = v \times t = 340 \times 1{,}23 = 418 \mathrm{m}\).
Les 418 m réel correspondent à une distance \(d^{'}_1 = 418 \times \frac{2,8}{100} = 11,7 \mathrm{cm}\). Il faut tracer sur la carte un cercle de rayon 11,7 cm à partir de l'office du tourisme.
Il y a alors deux intersections entre les deux cercles. Une passant sur une place et l'autre par un bâtiment qui est donc la position de Madeleine.